PacGAN
Outline
One of the major challenges in training Generative Adversarial Netowrks (GANs) is mode collapse, which collectively refers to the lack of divergence of the samples generated from the trained generator. Several heuristics have been proposed using ideas including minibatch discriminators, two sample testing, moment matching, and inverse mappings of the generator. In this project, we propose a principled approach to understand the connection between mode collapse and packing, showing multiple samples simulataneously at the dsicriminator input. This intuition that packing should help mitigate mode collapse has been around since the original minibatch discriminator of “Improved techniques for training GANs”, by Salimans, Goodfellow, Zaremba, Cheung, Radford, and Chen at NIPS 2016. We make this this intuition precise and make the following contributions:
Conceptual: We propose a mathematical definition of mode collapse, that allows us to measure how severe mode collapse is for a given pair of target distribution P and the genertor distribution Q. This allows one to formally compare two generators, in terms of how strong mode collapses they exhibit.
Anlaytical: We borrow proof techniques from Blackwell's seminal result in binary hypothesis testing in “Comparison of experiments” in 1951 and data processing inequalities from “The composition theorem for differential privacy” by Kairouz, Oh, and Viswanath, originally introduced for analyzing composition of differentially private mechanisms. This allows us to prove a fundamental connection between mode collapse and packing. In a nutshell, packed GAN naturally penalyzes those generators that exhibit strong mode collapse, thus encouraging PacGAN to learn a non-mode-collapsing generators.
Experimental: We propose a simple architectural change that can be applied to any standard GANs. The simplicity of the proposed architecture allows one to focus on the gains that are resulting from the ida of packing. We measure the gain of packing in benchmarkdatasets where quantifiable empirical measure of mode collapse has been introduced in the GAN literature, including synthetic mixture of Gaussians, stacked MNIST, and CelebA. We show how packing improves mode collapse in all such benchmakr datasets, using the experimental settings, hyper parameters, and the codes from existing literature, for fair comparisons.
You can find our paper here, code here, and the slides here that we used in recent talks we gave at NIPS workshop, MSR, UIUC, Michigan, Princeton, MIT, and Austin.
Check out an interview we did with Alex Lamb (MILA) on PacGAN, who provided us a lot of insights and constructive feedback on our work.
We plan to put a link to a talk on PacGAN soon.
Main idea behind PacGAN
We believe that one of the main reasons GANs suffer from mode collapse is because most of the popular GANs unnecessarily restrict the discriminator to be a function of a single input. In other words, diversity (or lack of diversity) in the generated samples is easier to detect if the discriminator is allowed to make the decision based on multiple samples jointly. This idea itself is not new. For example, this idea has been introduced and implemented in minibatch discriminator by Salimans et al. in “Improved Techniques for Training GANs”, covariance in each minibatch by Kerras et al. in “Progressive growing of gans for improved quality, stability, and variation”, and distributional adversary in by Li et al. in “distributional Adversarial Networks”. Our main contribution is in making this informal intuition formal, by introducing a mathematical definition of mode collapse, and proving that packing naturally penalizes severe mode collapse.
When implementing this idea of packing in all our experiments, we make minimal changes to a given mother architecture as follows. The reason is that we only want to demonstrate the effects of packing and nothing else. Hence, we keep everything the same as the baseline mother architecture (including all the hyper parameters in the training), and only make one change of increasing the input layer of the discriminator by a factor of m if we are packing m samples together as input to the discriminator.
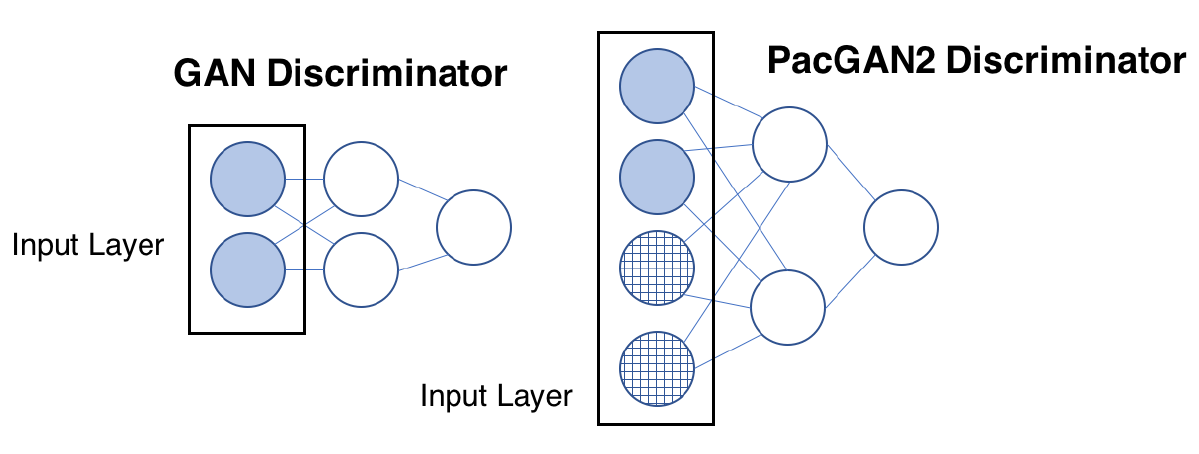 |
Toy example capturing the proof strategy
Our strategy to anlayze PacGAN is best explained via a toy example. Consider a discriminator trained with a 0-1 loss such that it provides an approximate loss fuction of total variation (where the quality of the approximation depends on the number of real samples, number of nodes in the discriminator, and the regulaization used in training th ediscriminator). We consider a toy example of real samples drawn from P, one-dimensional uniform distribution over [0,1], and two generator distributions denoted Q1 and Q2 with pdfs shown in the figure below.
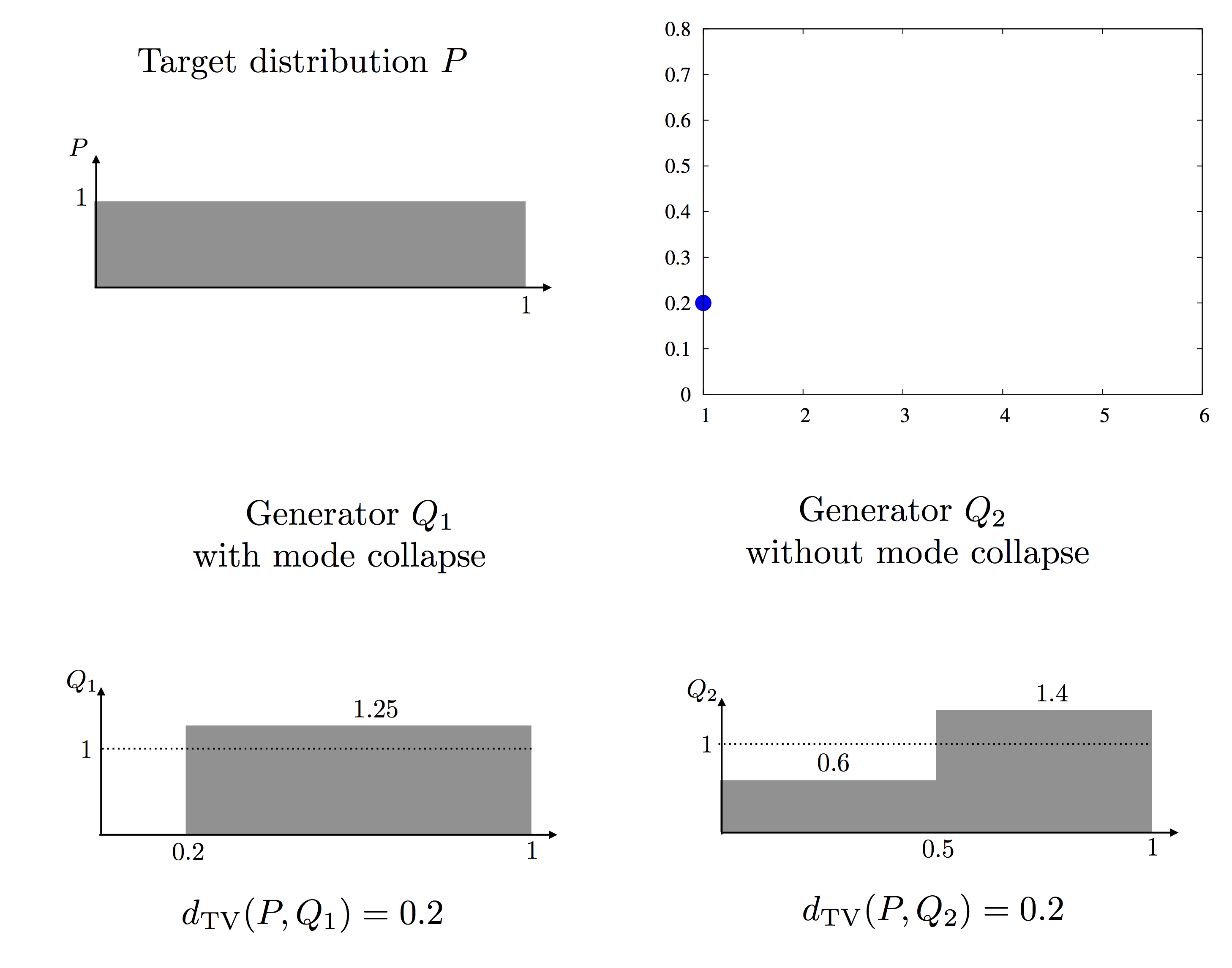 |
Q2 is a non mode collapsing generator distribution, as the perturbation from P is balanced out over the entire support. The specific values in the pdfs are chosen such that the total variation distances, TV(P,Q1) and TV(P,Q2), are the same (0.2 in this specific example). These two generators, therefore, achieve the same loss in training (unpacked) GAN and thus look the same in the generator training. However, something interesting happens when the GAN is packed. Consider packing two samples at the discrimiantor. This is essentially the same as taking one sample from the product distributions Q1*Q1 or Q2*Q2, as shown below. We can compute the total variation for the product distributions, also shown below. Note that the loss for the mode collapsing Q1 increases much faster when packing two samples together, compared to the non mode collapsing Q2.
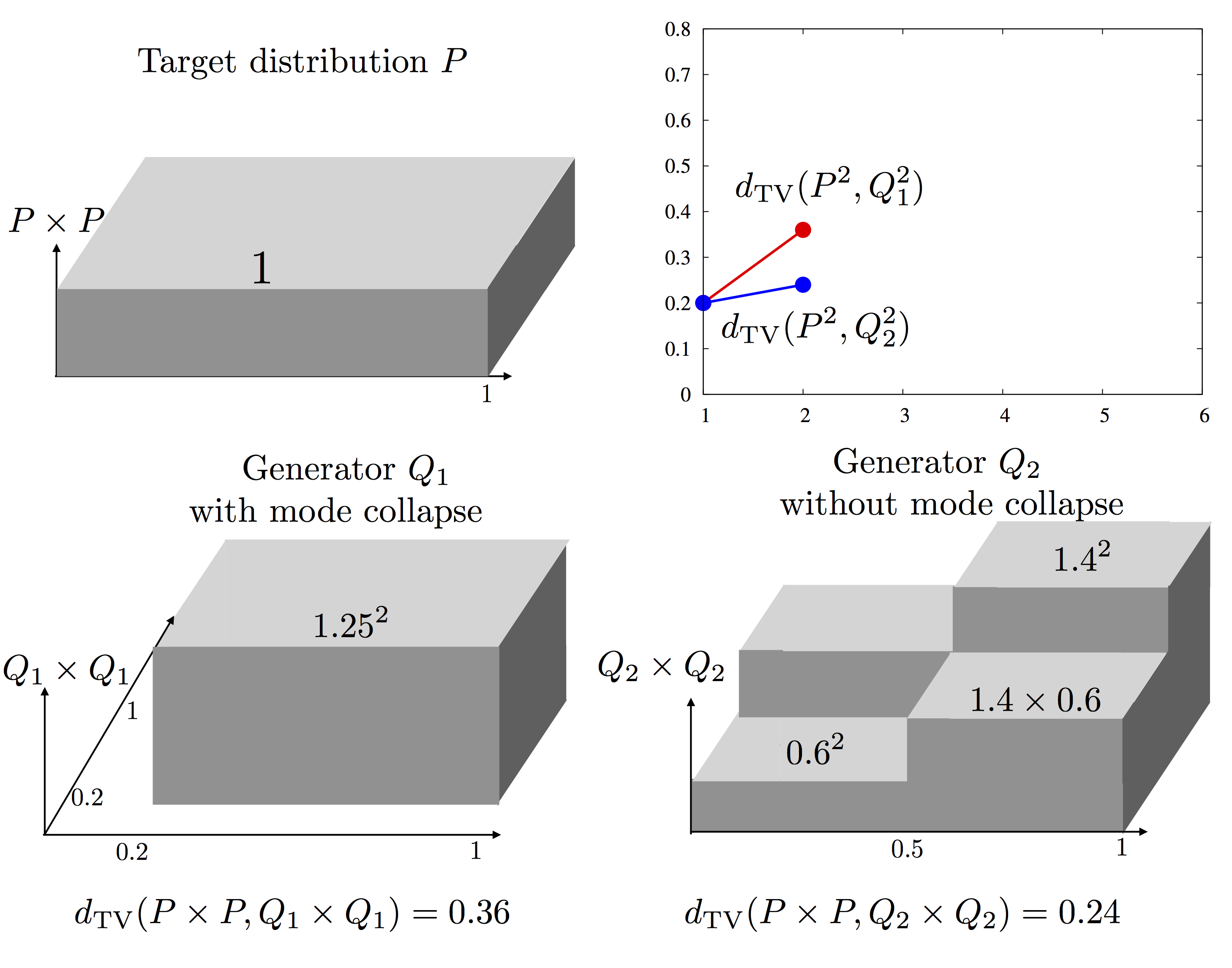 |
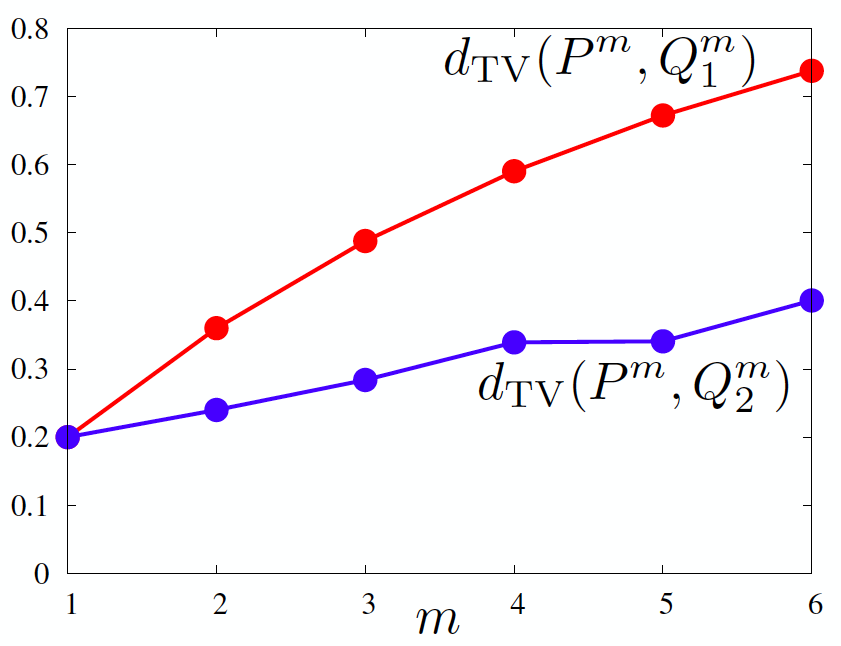
This trend continues in the evolution of total variation under packing, as shown below. While the two generators Q1 and Q2 looked the same to an unpacked GAN, the packed GAN penalizes Q1 more and hence encourages learning non mode collapsing Q2.
 |
Main idea of the proof
Experimental results
Q&A
Is there a gain for packing Wasserstein GAN (WGAN)?
This is a question asked by several people including Alex Lamb (MILA).
We do see some evidence that there should be packing gain for Wasserstein GANs with L2 distances.
Concretely, we can compute
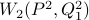 and
and 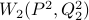 for
distributions Q1 and Q2 that are mode collapsing and non-mode collapsing, similar to the example above, but chosen such that the unpacked loss is the same:
for
distributions Q1 and Q2 that are mode collapsing and non-mode collapsing, similar to the example above, but chosen such that the unpacked loss is the same:
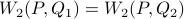 .
For this toy example, we observe that packed discriminator penalizes more
the mode-collapsing distribution:
.
For this toy example, we observe that packed discriminator penalizes more
the mode-collapsing distribution: 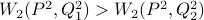 .
.
Can we be cheating on the discriminator size?
This is a question we asked ourselves. We again emphasize that we try our best to keep all the hyperparameters the same (as GAN that we are comparing with PacGAN, and as DCGAN that we are comparing with PacDCGAN). One of the hyper parameter that inevitably changes is the discriminator size. As shown below, we propose only increasing the input layer by m times, if we are packing m samples together. Usually this results in less than 5% increase in the number of parameters to be learned at the discriminator. Still, we were worried that some of the gains might be coming from this increased size of the discriminator, as predicted by the theoretical analysis of Arora et al in “Generalization and equilibrium in generative adversarial nets (GANs)” and empirically checked in “Do GANs learn the distribution? Some Theory and Empirics”.
 |
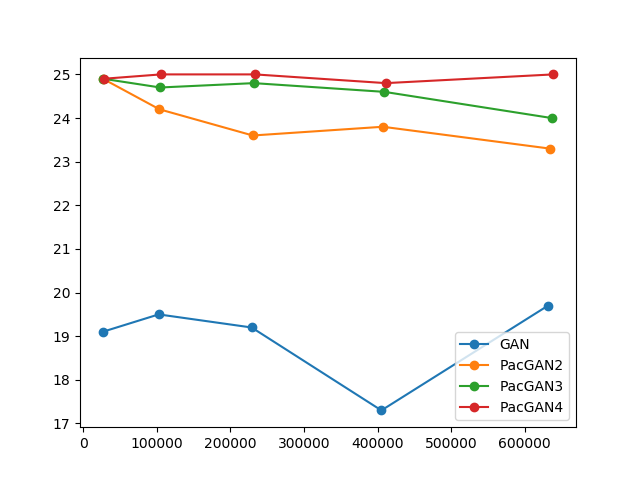
Shown in the figure below, we ran the 2D-grid experiments with varying size of the discriminators, to explicitly capture the effect of size of the discriminator. Perhaps surprisingly, we did not see much change in number of modes captures (y-axis) as a function of the number of parameters in the discriminator (x-axis). Such a phenomenon has been observed in Arora's experiments as well, when the size of the discriminator is already large enough that it is not the bottleneck in the perfomrance of the trained GAN. From Arora's experiments, we conjecture that if we keep decreasing the size of the discriminator, eventually we will see performance (in this case measured by the number of modes captured) will go down with decreasing discriminator size. But, more importantly, this implies that we are operating at a point where the discriminator size is not a bottle neck, and still an unpacked GAN exhibits significant mode collapse. PacGANs, on the other hand, are able to overcome the shortcomings of a GAN, and achieve the remaining eprformance gain that cannot be gained by simply increasing the discriminator sizes. This suggests that packing gain is fundamental in providing the extra gain not attainable by larger dsicriminators.
 |
Can we be cheating on the minibatch size in stochastic gradient descent?
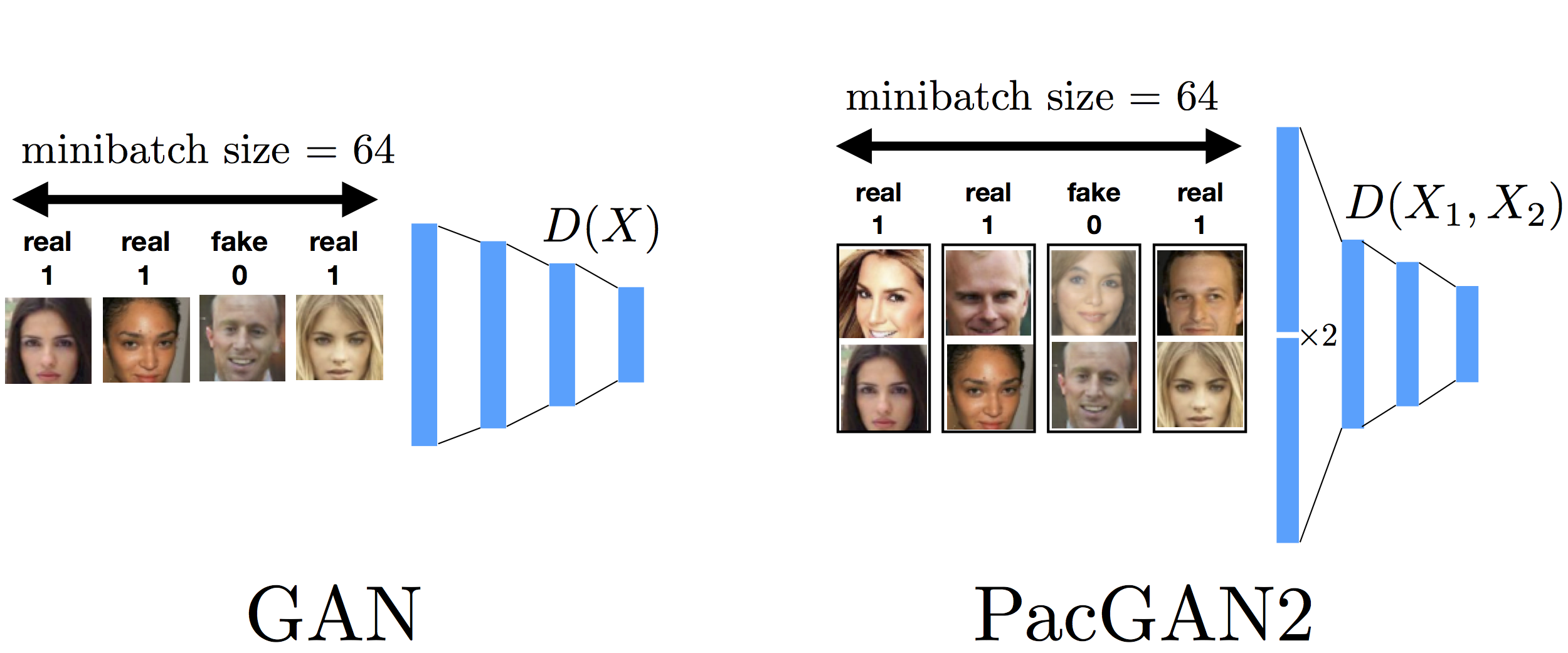
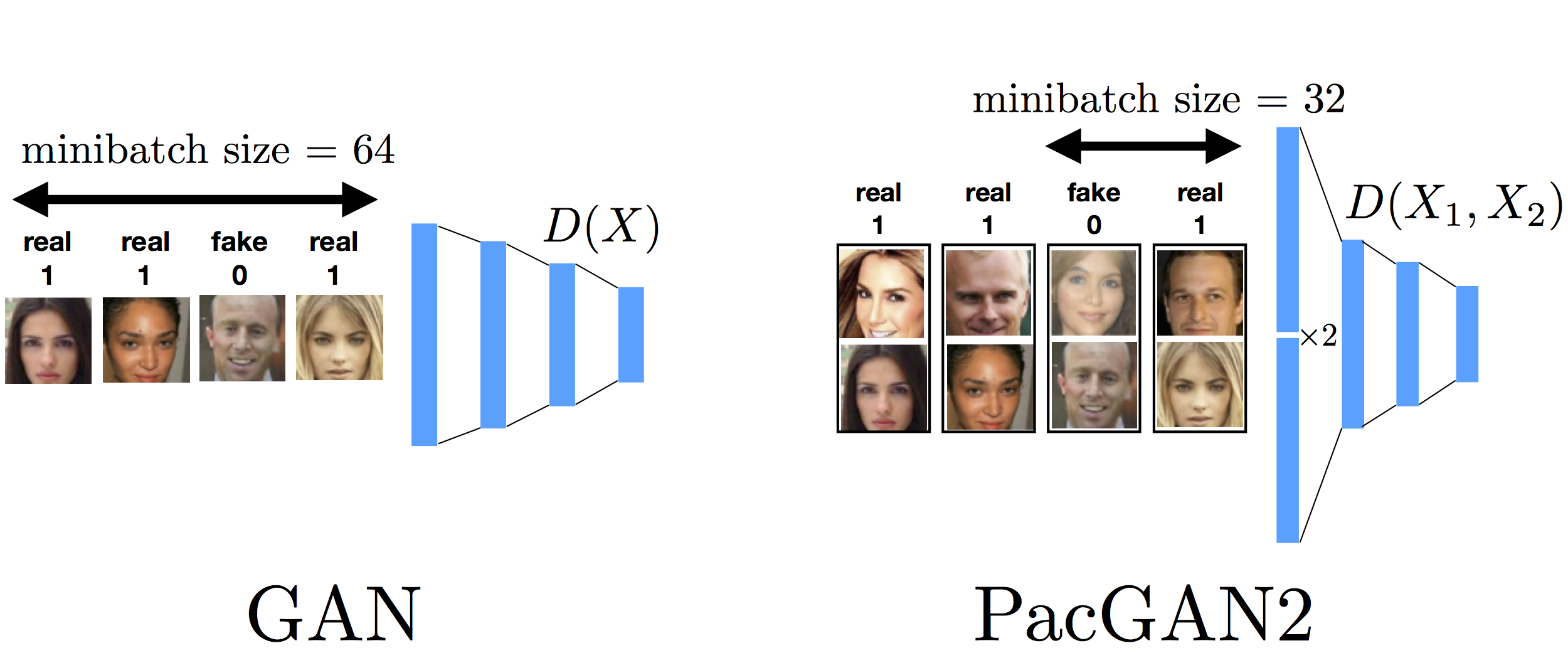
This is a question asked by Murat Kocaoglu (UT Austin). When packing a given mother architecture for empirical comparisons, we were careful in trying to match all hyperparameters used in training. However, there is one hyperparameter that is tricky, which is the minibatch size in the stochastic gradient update. Initially, we matched the minibatch size (for example averaging over 64 sampled gradients for both GAN and PacGAN2) as shown in the figure above. The reasoning for this choice was that we thought it is fair to have the same number of gradient computation per minibatch for both GAN and PacGAN. However, a question was raised that PacGAN now sees twice as more samples to perform one gradient update, and the gain might be coming from this increased effective minibatch size, which was not our intention.
To address this concern, we redid some of the experiments with the following minibatch update shown below. We make the minibatch size smaller (by a factor of two) for PacGAN2, such that the number of samples seen by the disciminator per gradient update is the same. Notice that now this is in some sense unfair to the PacGAN2 as we are allowing half as much computation (to compute the gradient). Even then, we observed for the stacked MNIST experiment as per VEEGAN setting that this choice of minibatch size allows PacGAN2 to recover all 1000 modes always.
 |
Is there packing gain in larger datasets, like CIFAR-10, CelebA, and ImageNet?
We are interested in mode collapse. The only large dataset we know of that has been evaluated with a quantifiable measure of mode collapse is CelebA, evaluated in “Do GANs learn the distribution? Some Theory and Empirics” by Arora et al.. The proposed metric of diversity (and hence mode collapse) is probability of seeing a collision among n generated samples from a trained generator. A collision is a pair of samples that are very similar (almost identical). Being similar is a subjective concept and Arora et al. propose a human evaluation (aided by machines to propose candidate images that are similar). The idea is that if collision happens then that implies that the generated samples are not diverse enough. The probability of collision (or equivalently the number of samples n such that the probability of collision is, say, 1/2) can be used as a measure of diversity in the generated samples.
We train DCGAN and PacDCGAN2 on CelebA dataset, and evaluate the probability of collision for various sizes of the discriminator. We emphasize here that it is critical to run these experiments blindly, as the prposed metric relies on human evaluation. We made sure that the human evaluators were not aware of which generator generated those samples that were to be evaluated. The table below shows that for various disscriminator sizes, PacDCGAN2 has a smaller collision probability, implying that the PacGAN2 generated more diverse samples.
| discriminator size | probability of collision | probability of collision |
| DCGAN | PacDCGAN2 | |
| d | 1 | 0.3 |
| 4d | 0.4 | 0 |
| 16d | 0.8 | 0 |
| 25d | 0.6 | 0.2 |
What is the connection to MMD-GAN and CramerGAN?